단축연산
비트 연산자 &와 | 는 논리연산자로 이용할 수 있다.
&&와 || 은 단축 연산을 수행한다.
단축 연산은 먼저 수행하는 피연산자의 결과가 결정되면 뒤에 오는 피연산자는 평가하지 않는다.
일반연산 프로그램

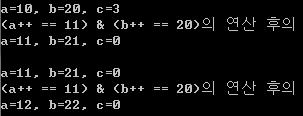
단축연산 프로그램


조건 연산자
조건연산자는 C언어 중 유일한 3개의 피연산자를 갖는 삼항 연산자.
exp1 ? exp2 : exp3
연산식 exp1이 0이 아닌 값(참)으로 평가되면,
삼항 연산자의 평가값은 두 번째 연산식인 exp2의 값으로 평가된다.
연산식 exp1이 0(거짓)으로 평가되면,
삼항 연산자의 평가값은 세 번째 연산식인 exp3의 값으로 평가된다.
변수 x의 절대값을 변수 absolute에 저장
absolute = (x<0) ? -x : x;
absolute = (x<0) ? -x : x;
큰 수와 작은 수


위의 방법은 2가지로 할 수 있다.
1. 지시자 형태로 아래와 같이 표현한다.
#define MAX(x,y) ((x<y) ? y : x)
2. 프로그램 속에서 한 줄로 표현하는 방법이 있다.
printf("두 수 (%d, %d) 중에서 작은 수는 %d이다.\n", a, b, a < b ? a : b);
one비트의 개념
one byte(8bit)가 출력이 될때 (8비트개념)
마이크로 <-----> 장치
프로세서
8비트라는게 8비트가 1비트씩 가냐? 한꺼번에 모두 가냐?
8개의 신호가 한 번에 간다.
필요한 데이터만 원하고 나머지 데이터는 필요없다.
이것이 비트논리이다.
비트 논리 연산자
피연산자 정수 값(32비트)을 비트 단위로 논리 연산을 수행하는 연산자.
2진수 각 자리에 대해 연산
결과가 음수일 경우, 2의 보수로 바꾸고 10진수화 (XOR)
전체를 32비트(4byte)로 본다.
| 연산자 | 기호 |
| AND | x & y |
| OR | x | y |
| XOR | x ^ y |
| NOT | ~ x |
(3 & 5) == 1 (참과 참이므로 1이다 이렇게 생각할 수 있다.)
(7 & 5) == 5 (이 경우는 비트 논리로 볼 때 참이다)
3(10) -> 0011(2)
5(10) ->&) 0101(2)
1(10) -> 0001(2)
7(10) -> 0111(2)
5(10) ->&) 0101(2)
5(10) -> 0101(2)
1비트에 대한 개념이다.
장비에서 스위치 값을 쓰거나
led를 점등시키려 할때
한 선로의 개념을 가져가야 한다.


3(10) -> 0011(2)
5(10) -> |) 0101(2)
7(10) -> 0111(2)
3(10) -> 0011(2)
5(10) ->^) 0101(2)
6(10) -> 0110(2)
여기서 문제는 ~3과 ~5이다.
~3(10) -> ~(0011(2))를 32비트로 표현하면
32비트 : 00000000 00000000 00000000 00000011(2) (십진수 3)
여기서 not이므로
32비트 : 11111111 11111111 11111111 11111100(2) (십진수 -3)
첫 비트가 0이면 양수
첫 비트가 1이면 음수
음수를 표현할 방법은 2의 보수를 이용한다.
1의보수를 구한다.
32비트 : 00000000 00000000 00000000 00000011 (십진수 -3)
+1 (2의보수)
32비트 : 00000000 00000000 00000000 00000100 (십진수 4)
부호가 - 이므로 -4로 한다.
5(10) -> 00000000 00000000 00000000 00000101
~5(10) -> 11111111 11111111 11111111 11111010
1의보수 -> 00000000 00000000 00000000 00000101
2의보수 -> 00000000 00000000 00000000 00000110
----------------------------------------------------------
결과 값은 -6
~3는 -4
~5는 -6
미루어 생각하면
~2는 -3
~7는 -8
이동 연산자
비트 단위로 왼쪽이나 오른쪽으로 이동시키는 연산자
이동 후 좌우측 경계를 벗어난 비트는 무시하고, 오른쪽의 빈 비트는 0을 채우고, 왼쪽은 부호비트를 채운다.
| 연산자 | 기호 | 의미 |
| 왼쪽 이동 연산자 | << | shift left |
| 오른쪽 이동 연산자 | >> | shift right |
00~00 7(10) -> 0000 0111
00~00 14(10) -> 0000 1110
00~00 28(10) -> 0001 1100


c언어를 오른쪽으로 이동하면
8 -> 4 -> 2로 반씩 줄어든다.
7 -> 3(3.5) -> 1(1.5)로 반씩 줄어든다.
000 7(10) -> 0000 0111
000 3(10) -> 0000 0011
000 1(10) -> 0000 0001
000 8(10) -> 0000 1000
000 4(10) -> 0000 0100
000 2(10) -> 0000 0010
어셀블이어를 오른쪽으로 이동하면
1100 1001
-> 1100 100 1(떨어진 1이 왼쪽으로 붙는다.)
-> 1110 0100
어셀블이어를 왼쪽으로 이동하면
1100 1001
-> 100 10011
-7 >> 2 (-7을 두자리 이동시키면)
?(10) -> 11111111 11111111 11111111 1111 _ _ _ _
1의보수 -> 00000000 00000000 00000000 0000 0110
2의보수 -> 00000000 00000000 00000000 0000 0111 (-7)
원래의 수(10) -> 11111111 11111111 11111111 1111 1001
1번이동 => 1 11111111 11111111 11111111 1111 100 (1은 부호비트)
1번이동 -> 11 11111111 11111111 11111111 1111 10 (1은 부호비트)
위의 숫자는 음수이므로 2의 보수로 바꾸면
두자리 이동한 수가 된다.
1의 보수 00000000 00000000 00000000 00000001
2의 보수 + 1
이동한 값 00000000 00000000 00000000 00000010 (-2)
[ 문제 ]
-9 >> 3
-9는 어떤 수인가 뭔가 찾은게 -9라는 것이다.
원래의 수는 ?
원수(10)-> 11111111 11111111 11111111 1111 _ _ _ _
1의보수 -> 00000000 00000000 00000000 0000 1000
2의보수 -> 00000000 00000000 00000000 0000 1001 (-9)
-> 11111111 11111111 11111111 1111 0111
1번이동 -> 1 11111111 11111111 11111111 1111 011 (1은 부호비트)
1번이동 -> 11 11111111 11111111 11111111 1111 01 (1은 부호비트)
1번이동 -> 111 11111111 11111111 11111111 1111 0 (1은 부호비트)
위의 수는 음수이므로 2의 보수로 바꾸면 3자리 이동한 수가 나온다.
1의 보수 00000000 00000000 00000000 00000001
2의 보수 + 1
이동한 값 00000000 00000000 00000000 00000010 (-2)

9 << 3
9(10) -> 00000000 00000000 00000000 00001001
?(10) -> 00000000 00000000 00000000 01001000
이동한 값은 = 64 + 8 = 72

비트 이동 연산자(<< , >>)의 결과
참고 : http://prof.dongju.ac.kr/syhong/public_html/teaching/c/c04.htm
47과 -47을 3비트 이동한 결과를 보자


이동 연산자의 계산
오른쪽 이동 연산자는 비트 이동을 한 번 할 때마다 연산자를 2로 나누는 효과
왼쪽쪽 이동 연산자는 비트 이동을 한 번 할 때마다 연산자를 2로 곱하는 효과
a >> b의 결과는 a / 2^b (a가 양수인 경우)
a << b의 결과는 a * 2^b
9 << 3의 결과는 9 * 2^3 = 72
축약 대입 연산자
대입 연산자와 산술연산자를 합쳐 놓은 듯한 연산자
왼쪽 피연산자 위치는 변수만 올 수 있다.
x = 3;
y = 3;
x += y + 3 * 4;
-> x + (y + 3 * 4);
연산 평가 값 x = 19

| 축약 대입 연산자 | 의미 |
| x += y | x = x + y |
| x -= y | x = x - y |
| x *= y | x = x * y |
| x /= y | x = x / y |
| x %= y | x = x % y |
| x &= y | x = x & y |
| x |=y | x = x | y |
| x ^= y | x = x^y |
| x >>= y | x = x >> y |
| x <<= y | x = x << y |

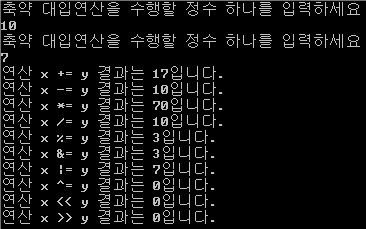
10과 7을 입력한다.
X는 이전 값이 계속 남아 있다.

'자동제어 > PC 제어' 카테고리의 다른 글
| PC제어프로그램 1일차 (200417) (0) | 2020.06.17 |
|---|---|
| PC제어프로그램 7일차 (20.05.28) - 기본코딩2 (0) | 2020.05.28 |
| visual studio c++ 프로그래밍 코드를 웹에서 테스트 할 수 있다. (1) | 2020.05.21 |
| PC제어프로그램 6일차 (20.05.21) - 기본코딩1 (0) | 2020.05.21 |
| 윈도우 7 이상에서 Visual Studio 6.0 설치 (0) | 2020.05.16 |


